Clustering algorithms
Contents
Clustering is a unsupervised Machine Learning algorithm that groups a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). [Suggested introductory reading]. Here, I shall talk about three of them namely EM clustering, k-means and hierarchical clustering.
EM clustering
We have $N$ data samples (unlabelled) $D= { x_1,x_2,\dots,x_N } $ spanning $c$ classes $w_1,w_2,\dots,w_c$. In order to simplify our analysis let’s assume $c=3$ and $N=500$. We can write the prior and likelihood as follows
| Prior | Likelihood |
|---|---|
| $P(w_1)$ | $P(x/w_1) \sim \mathcal{N}(\mu_1,\sum_1)$ |
| $P(w_2)$ | $P(x/w_2) \sim \mathcal{N}(\mu_2,\sum_2)$ |
| $P(w_3)$ | $P(x/w_3) \sim \mathcal{N}(\mu_3,\sum_3)$ |
Gaussian Mixture Model (GMM)
The problem can be formulated as a GMM
\[P(x/\theta)=P(w_1)P(x/w_1)+P(w_2)P(x/w_2)+P(w_3)P(x/w_3)\]Given, the data points $ { x_1,x_2,\dots,x_N } $ our goal is to find the parameter $\theta$ (consists of $\mu_i \text{, } \sum_i \text{ and } P(w_i)$) using MLE (ML Estimation).
Expectation maximization to solve GMM parameters
We can find the parameters using an iterative scheme. We can initialize $(\mu_i,\sum_i)$ with some random values and then iterate over the expectation and maximization steps until convergance is achieved.
Expectation
Assuing $(\mu_1,\sum_1)$ are available, we can perform Bayesian classification on $ { x_1,x_2,\dots,x_n } $ using likelihood at some iteration as
\[x_k \in w_i \text{ iff } P(x_k/w_i)>P(x_k/w_j) \forall j \neq i\]Maximization
Given some $x_k$, then what are $(\mu_i,\sum_i)$ that maximize for those $x_k$ to have $P(x_k/w_i) \sim \mathcal{N}(\mu_i,\sum_i)$?
\[\{ x_1,x_2,\dots,x_n \} \in w_i\]Using MLE,
\(\mu_i = \frac{1}{N_i} \sum_k x_k \forall x_k \in w_i\) \(\sum_i = \frac{1}{N_i} \sum_k (x_k-\mu_i)(x_k-\mu_i)^T \forall x_k \in w_i\)
Thus, we have the updated values for $(\mu_i,\sum_i)$ and can now again perform expectation step in an iterative way untill convergance.
k-means clustering
Let us assume identity covarience matrix i.e. $ | \sum | = 1 $, we can write
\(P(x_k/w_i) = \frac{1}{(2\pi)^{d/2}} e^{ \frac{-1}{2} (x_k-\mu_i)^T (x_k-\mu_i)} = \frac{1}{(2\pi)^{d/2}} e^{ \frac{-1}{2} \| x_k-\mu_i \| ^2 }\)
Algorithm
- Descide the number of clusters, $c$
- Assume $\mu_i$ for classes $1:c$
- Expectation
- \(x_k \in\) if \(P(x_k/w_i)>P(x_k/w_j) \forall i \neq j\)
- if \(\| x_k-\mu_i \| ^2 \leq \| x_k-\mu_j \| ^2 \forall i \neq j, \text{ then } x_k \in w_i\)
- Maximization \(\mu_i = \frac{1}{N_i} \sum_k x_k \forall x_k \in w_i\)
- Repeat step 2 and 3 untill convergence, \(\| \mu_i^t-\mu_i^{t-1} \| ^2 \to \text{constant}\)
Below code shows the implementation
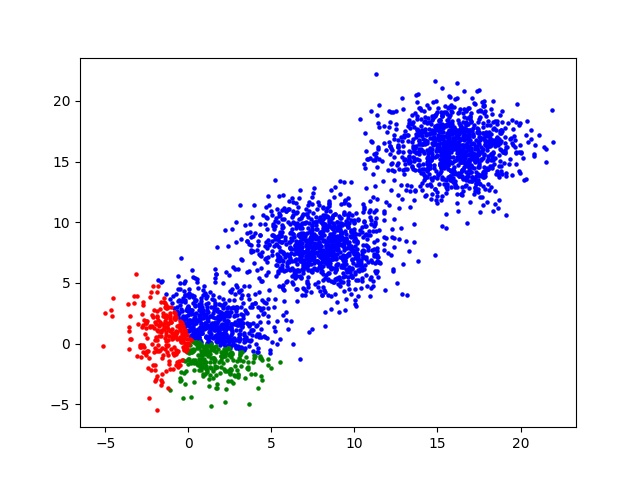
Fig.1: Initial iteration using k-means
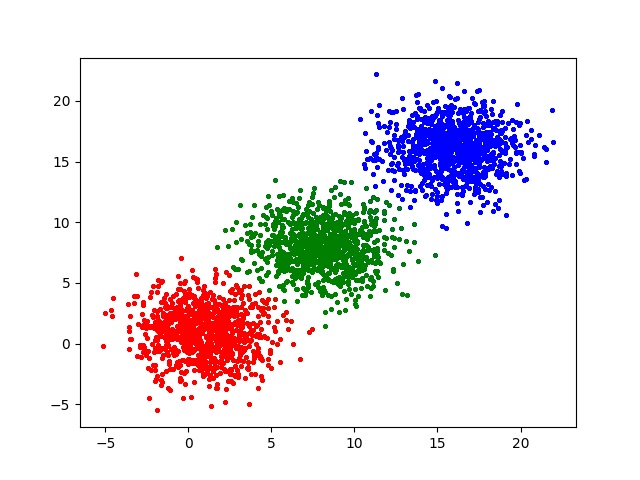
Fig.2: Final clusters obtained via k-means
As shown in the above two figures the k-means algorithm correctly clusters the data points into three clusters.
Hierarchical clustering
Hierarchical clustering is a clustering method which seeks to build a hierarchy of clusters based on some distance or similarity meteric. This can be further classified as
- Agglomerative clustering: (“bottom-up” approach) each point starts as a seperate individual cluster and merges into a single cluster.
- Divisive clustering: (“top-down” approach) starts with one single cluster and keeps on dividing upto individual point clusters
- Isodata clustering: combines features of both agglomerative and divisive clustering to achieve optimal clusters
Based on the distance meteric used the agglomerative clustering can be further classified as
- Single link or Nearest neighbour
- Distance between two clusters $c_1$ and $c_2$, $d = \min | X-Y |^2 \text{ where, } X \in c_1 \text{ and } Y \in c_2 $
- Complete link or farthest neighbour
- Distance between two clusters $c_1$ and $c_2$, $d = \max | X-Y |^2 \text{ where, } X \in c_1 \text{ and } Y \in c_2 $
Example: Single Link
Suppose that we have the given points $x_1,x2,\dots,x7$ with the distances shown below.
x1 ------- x2 ------- x3 ------- x4 ------- x5 ------- x6 ------- x7
1 1.1 1.2 1.3 1.4 1.5
To form clusters, we treat the individual points as clusters and grow them. Find the distance between the clusters using $d = \min | X-Y |^2 \text{ where, } X \in c_1 \text{ and } Y \in c_2 $ and merge $c_i$ with $c_j$ if $d(c_i,c_j) \leq d(c_i,c_k) \forall k \neq j $. Finally we can obtain
x1 x2 x3 x4 x5 x6 x7
| | | | | | |
| | | | | | |
------------ 1 | | | | |
| | | | | |
| | | | | |
------------------ 1.1 | | | |
| | | | |
| | | | |
--------------------- 1.2 | | |
| | | |
| | | |
--------------------- 1.3 | |
| | |
| | |
--------------------- 1.4 |
| |
| |
---------------------- 1.5
Example: Complete Link
We can use the same example distances given in single link example. Here, we can find the distance between the clusters using $d = \max | X-Y |^2 \text{ where, } X \in c_1 \text{ and } Y \in c_2 $ and merge $c_i$ with $c_j$ if $d(c_i,c_j) \leq d(c_i,c_k) \forall k \neq j $. Finally we can obtain
x1 x2 x3 x4 x5 x6 x7
| | | | | | |
| | | | | | |
------------ 1 | | | | |
| ------------- 1.2 | | |
| | ------------ 1.4 |
| | | |
| | | |
| | ----------------- 2.9
------------------------ 3.3 |
| |
| |
--------------------------------------------- 7.5